Deep learning for NeuroImaging in Python.

Note

This page is a reference documentation. It only explains the class signature, and not how to use it. Please refer to the gallery for the big picture.

class nidl.estimators.autoencoders.vae.VAE(encoder: Module, decoder: Module, encoder_out_dim: int, latent_dim: int, beta: float = 1.0, default_dist: str = 'normal', stochastic_transform: bool = True, lr: float = 0.0001, weight_decay: float = 0.01, random_state: int | None = None, **kwargs)[source]¶

Bases: TransformerMixin, BaseEstimator

Variational Auto-Encoder (VAE) [R5] [R6].

See Also: BetaVAELoss

A VAE is a probabilistic generative model that learns a latent representation of input data and reconstructs it. It implements fit and transform methods to respectively train the model and obtain the latent embeddings.

The VAE consists of three main components:

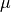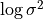
Encoder: maps input x to latent mean $\mu$ and log-variance $\log \sigma^2$
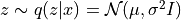
Reparameterization trick: samples latent vector $z \sim q(z | x) = \mathcal{N}(\mu, \sigma^2 I)$
Decoder: reconstructs input 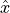$\hat{x}$ from latent vector $z$

The model is trained by minimizing the sum of two components:

Reconstruction loss: Measures how well the decoder reconstructs the input.
- For binary data: Binary Cross-Entropy (BCE) loss
- For continuous data: Mean Squared Error (MSE) loss
$\mathcal{L}_{recon} = - \mathbb{E}_{q(z|x)} [ \log p(x|z) ]$
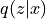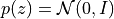KL Divergence loss: Encourages the latent distribution $q(z|x)$ to be close to the prior $p(z) = \mathcal{N}(0, I)$ .

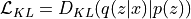
$\mathcal{L}_{KL} = D_{KL}(q(z|x) | p(z))$

The total loss is a weighted sum of these two components:

$\mathcal{L}_{total} = \mathcal{L}_{recon} + \beta \mathcal{L}_{KL}$

Parameters:

encoder : class:~torch.nn.Module

The encoder mapping input x to the representation space. The mean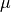 $\mu$ and log-variance 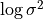$\log \sigma^2$ layers are automatically added according to the latent_dim parameter.

decoder : class:~torch.nn.Module

The decoder backbone outputting 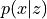$p(x | z)$ as a torch.distributions or a torch.Tensor representing the mean of a Normal (default) or Laplace distribution.

encoder_out_dim : int

The output size of the encoder.

latent_dim : int

The number of latent dimensions (which is the size of the mean and variance of the posterior distribution).

beta : float, default=1.

Scaling factor for Kullback-Leibler distance (beta-VAE).

default_dist : str, default=”normal”

Default decoder distribution. It defines the reconstruction loss (L2 for Normal, L1 for Laplace, cross-entropy for Bernoulli).

stochastic_transform : bool, default=True

If True (default), the transformed data are obtained by sampling according to the posterior distribution 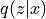$q(z | x)$ .If False, the mean of the posterior distribution is returned.

lr : float

the learning rate.

weight_decay : float

the Adam optimizer weight decay parameter.

random_state : int, default=None

setting a seed for reproducibility.

kwargs : dict

trainer parameters.

References

[R5] (1,2)

Diederik P. Kingma, Max Welling, “Auto-Encoding Variational Bayes”, ICLR 2014.

[R6] (1,2)

Irina Higgins et al., “beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework”, ICLR 2017.

Attributes

encoder	(`Module`) The encoder network.
decoder	(`Module`) The decoder network.
fc_mu	(`Module`) The linear layer mapping the encoder output to the mean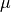 $\mu$ of the posterior distribution.
fc_logvar	(`Module`) The linear layer mapping the encoder output to the log-variance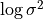 $\log \sigma^2$ of the posterior distribution.

configure_optimizers()[source]¶: Declare an AdamW optimizer.

forward(x: Tensor) → Tensor[source]¶

Encode the input and sample from the posterior distribution q(z|x).

Parameters:: x : torch.Tensor

Input data given to the encoder.
Returns:: z : torch.Tensor, shape (batch_size, latent_dim)

Latent vector sampled from the posterior distribution.

sample(n_samples)[source]¶

Generate n_samples by sampling from the latent space.

Parameters:: nsamples : int

Number of samples to generate.
Returns:: x : torch.Tensor

Generated samples.

training_step(batch: Tensor, batch_idx: int, dataloader_idx: int | None = 0)[source]¶

Perform one training step and computes and logs training losses.

Three losses are logged: the beta-VAE loss (“loss”), the reconstruction loss (“rec_loss”) and the KL divergence loss (“kl_loss”).

Parameters:

batch : torch.Tensor

The input data given to the encoder.

batch_idx : int

Ignored.

dataloader_idx : Optional[int], default=0

Ignored.

Returns:

losses : dict

Dictionary with “loss”, “rec_loss”, “kl_loss” as keys.

transform_step(batch: Tensor, batch_idx: int, dataloader_idx: int | None = 0)[source]¶

Transform the input data to the latent space.

By default, the latent vector is obtained by sampling according to the posterior distribution 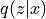$q(z | x)$ . It is just the mean of the distribution if stochastic_transform is False.

Parameters:

batch : torch.Tensor

The input data given to the encoder.

batch_idx : int

Ignored.

dataloader_idx : Optional[int], default=0

Ignored.

Returns:

z : torch.Tensor, shape (batch_size, latent_dim)

The latent vector.

validation_step(batch: Tensor, batch_idx: int, dataloader_idx: int | None = 0)[source]¶

Perform one validation step and computes and logs validation losses.

Three losses are logged: the beta-VAE loss (“loss”), the reconstruction loss (“rec_loss”) and the KL divergence loss (“kl_loss”).

Parameters:

batch : torch.Tensor

The input data given to the encoder.

batch_idx : int

Ignored.

dataloader_idx : Optional[int], default=0

Ignored.

Returns:

losses : dict

Dictionary with “loss”, “rec_loss”, “kl_loss” as keys.