Deep learning for NeuroImaging in Python.

Note

This page is a reference documentation. It only explains the class signature, and not how to use it. Please refer to the gallery for the big picture.

class nidl.estimators.ssl.simclr.SimCLR(encoder: Module, hidden_dims: Sequence[str], lr: float, temperature: float, weight_decay: float, random_state: int | None = None, **kwargs)[source]¶

Bases: TransformerMixin, BaseEstimator

SimCLR [R12].

SimCLR is a contrastive learning framework for self-supervised representation learning. The key idea is to learn useful features without labels by making different augmented views of the same image close in a representation space, while pushing apart representations of different images. Once trained, the encoder can be reused for downstream tasks such as classification or regression.

The model consists of:

A base encoder f (e.g., a CNN), which extracts representation vectors.
A projection head g, which maps representations into a space where the contrastive objective is applied.

During training, two augmented versions of each input x are encoded into (z_i, z_j). The objective is to maximize their similarity while minimizing similarity to all other samples in the batch. This is achieved with the InfoNCE loss [R13], [R14]:

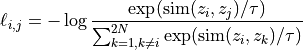
$\ell_{i,j} = -\log \frac{\exp(\text{sim}(z_i, z_j)/\tau)} {\sum_{k=1, k\neq i}^{2N} \exp(\text{sim}(z_i, z_k)/\tau)}$

Similarity is measured with cosine similarity. The temperature 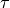$\tau$ controls the sharpness of the distribution (refer to [R15] for more details). After training, the projection head g is discarded, and the encoder f serves as a pretrained feature extractor. This is because f provides representations that transfer better to downstream tasks than those from g.

Parameters:

encoder : nn.Module

the encoder f. It must store the size of the encoded one-dimensional feature vector in a latent_size parameter.

hidden_dims : list of str

the projector g with an MLP architecture.

lr : float

the learning rate.

temperature : float

the SimCLR loss temperature parameter.

weight_decay : float

the Adam optimizer weight decay parameter.

max_epochs : int, default=None

optionaly, use a CosineAnnealingLR scheduler.

random_state : int, default=None

setting a seed for reproducibility.

kwargs : dict

Trainer parameters.

References

[R12] (1,2)

Ting Chen, Simon Kornblith, Mohammad Norouzi, Geoffrey Hinton, “A Simple Framework for Contrastive Learning of Visual Representations”, ICML 2020.

[R13] (1,2)

Aaron van den Oord, Yazhe Li, Oriol Vinyals, “Representation Learning with Contrastive Predictive Coding”, arXiv 2018.

[R14] (1,2)

Sohn Kihyuk, “Improved Deep Metric Learning with Multi-class N-pair Loss Objective”, NIPS 2016.

[R15] (1,2)

Feng Wang, Huaping Liu, “Understanding the Behaviour of Contrastive Loss”, CVPR 2021.

Attributes

f	a `Module` containing the encoder.
g	a `Module` containing the projection head.

all_gather_and_flatten(tensor: Tensor, **kwargs)[source]¶

Gathers the tensor from all devices and flattens batch dimension.

This is useful when gathering tensors without adding extra dimensions. It handles some edge cases, such as when using a single GPU.

Parameters:

tensor : torch.Tensor

The tensor to gather.

**kwargs : dict

Additional keyword arguments for self.all_gather.

Returns:

tensor : torch.Tensor

The gathered and flattened tensor.

configure_optimizers()[source]¶: Declare a AdamW optimizer and, optionally a CosineAnnealingLR learning rate scheduler if max_epochs is set.

training_step(batch: tuple[Tensor, Tensor], batch_idx: int, dataloader_idx: int | None = 0)[source]¶

Perform one training step and computes training loss.

Parameters:

batch : Any

A batch of data that has been generated from train_dataloader. It should be a pair of torch.Tensor (V1, V2) where V1 and V2 are the two views of the same sample. They must have equal first dimensions.

batch_idx : int

The index of the current batch (ignored).

dataloader_idx : int, default=0

The index of the dataloader (ignored).

Returns:

loss : Tensor

Training loss computed on this batch of data.

transform_step(batch: Tensor, batch_idx: int, dataloader_idx: int | None = 0)[source]¶

Encode the input data into the latent space.

Importantly, we do not apply the projection head here since it is not part of the final model at inference time (only used for training).

Parameters:

batch : torch.Tensor

A batch of data that has been generated from test_dataloader. This is given as is to the encoder.

batch_idx : int

The index of the current batch (ignored).

dataloader_idx : int, default=0

The index of the dataloader (ignored).

Returns:

features : torch.Tensor

The encoded features returned by the encoder.

validation_step(batch: tuple[Tensor, Tensor], batch_idx: int, dataloader_idx: int | None = 0)[source]¶

Perform one validation step and computes validation loss.

Parameters:

batch : Any

A batch of data that has been generated from val_dataloader. It should be a pair of torch.Tensor (V1, V2).

batch_idx : int

The index of the current batch (ignored).

dataloader_idx : int, default=0

The index of the dataloader (ignored).

Examples¶

Model probing callback of embedding estimators

Self-Supervised Contrastive Learning with SimCLR