Deep learning for NeuroImaging in Python.

Note

This page is a reference documentation. It only explains the class signature, and not how to use it. Please refer to the gallery for the big picture.

class nidl.losses.beta_vae.BetaVAELoss(beta: float = 4.0, default_dist: str = 'normal')[source]¶

Bases: object

Compute the Beta-VAE loss [R29].

See Also: VAE

The Beta-VAE was introduced to learn disentangled representations and improve interpretability. The idea is to keep the distance between the real and estimated posterior distribution small (under a small constant delta) while maximizing the probability of generating real data:

$\underset{\phi, \theta}{\mathrm{max}} \underset{x \sim D}{\mathbb{E}}\left[ \underset{z \sim q_\phi(z | x)}{\mathbb{E}} log \ p_\theta(x|z) \right] \\ \text{subject to} D_{KL}(q_\phi(z|x) | p_\theta(z)) < \delta$

We can rewrite this equation as a Lagrangian with a Lagrangian multiplier 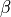$\beta$ , which leads to the Beta-VAE loss function: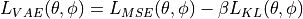

$L_{VAE}(\theta, \phi) = L_{MSE}(\theta, \phi) - \beta L_{KL}(\theta, \phi)$

When 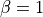$\beta=1$ , it corresponds to a VAE loss. If 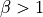$\beta>1$ , this puts more weight on statistical independence than on reconstruction. Note that such a stronger constraint on the latent bottleneck limits the representation capacity of z.

Parameters:

beta : float, default=4.0

Weight of the KL divergence.

default_dist : {“normal”, “laplace”, “bernoulli”}, default=”normal”

Default decoder distribution. It defines the reconstruction loss (L2 for Normal, L1 for Laplace, cross-entropy for Bernoulli).

Raises:

ValueError

If the input distribution is not supported.

References

[R29] (1,2)

Irina Higgins et al., “beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework”, ICLR 2017.

kl_normal_loss(q)[source]¶

Computes the KL divergence between a normal distribution with diagonal covariance and a unit normal distribution.

Parameters:: q : torch.distributions

probabilistic encoder (or estimated posterior probability function).

reconstruction_loss(p, data)[source]¶

Computes the per image reconstruction loss for a batch of data (i.e. negative log likelihood).

The distribution of the likelihood on the each pixel implicitely defines the loss. Bernoulli corresponds to a binary cross entropy. Gaussian distribution corresponds to MSE. Laplace distribution corresponds to L1.

Parameters:

p : torch.distributions

probabilistic decoder (or likelihood of generating true data sample given the latent code).

data : torch.Tensor

The observed data.

Returns:

loss : torch.Tensor

per image cross entropy (i.e. normalized per batch but not pixel and channel).